Logic programming is a simple, yet powerful formalism suitable for programming and knowledge representation [1]. A logic program is represented by a set of facts, and rules describing how new facts can be generated from the existing ones. Logic programming allows the developer to focus on devising facts and rules of a logical derivation, and not on algorithms and their optimizations, which are delegated to the underlying logic deduction engine. The most striking feature of logic programming for the newcomer is how much simpler the programs look than in other languages [2]. Datalog [3] is one of the most famous logic programming languages, designed for working with databases.
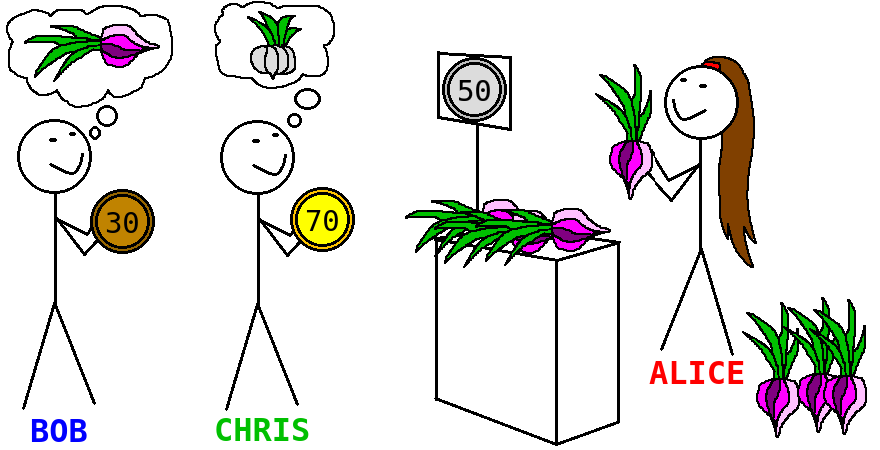
As an example, let us construct a Datalog script for a simple auction application. First of all, we need to come up with a list of facts. We have a set of buyers and a set of sellers (these sets may overlap). Each seller declares which products they sell at which price.
sells("bob", "garlic", 30).
sells("bob", "onion", 50).
sells("chris", "garlic", 70).
Similarly, each buyer declares which product they want to buy at which price.
buys("alice", "garlic", 50).
buys("bob", "carrot", 70).
We want to express a rule ''bargain(Buyer,Seller,Product)'', which is true if and only if the ''Buyer'' can buy from the ''Seller'' the ''Product''. We need to come up with a list of conditions that need to be satisfied for ''bargain(Buyer,Seller,Product)'' to be true. A bargain between the ''Buyer'' and the ''Seller'' w.r.t. ''Product'' is considered successful if the money ''Budget'' that the ''Buyer'' is ready to spend is at least the ''Cost'' at which the ''Seller'' sells the ''Product''. To make the rule more interesting, let us assume that the ''Cost'' is given without taking into account the tax, and there is known to be a certain ''Tax'' that depends on the type of ''Product''. We get the following rule.
bargain(Buyer,Seller,Product) :-
buys(Buyer,Product,Budget),
sells(Seller,Product,Cost),
tax(Product,Tax),
Budget >= Cost * (1 + Tax).
We have not yet specified what ''tax(Product,Tax)'' means. In logic programming, a rule may in turn depend on the other rules, so let us describe the rules for ''tax''. We assume that there are three possible choices of products (carrot, garlic, and onion), each having its own tax.
tax(Product, Tax) :-
Product = "carrot",
Tax = 0.1.
tax(Product, Tax) :-
Product = "garlic",
Tax = 0.2.
tax(Product, Tax) :-
Product = "onion",
Tax = 0.3.
Finally, we need to state a question that the logic programming engine has to answer. Let us ask who can sell garlic to Alice.
?- bargain("alice", Seller, "garlic").
Based on the facts and rules above, Datalog answers that one (and the only one) potential seller is Bob.
Seller = "bob"
Indeed, there is Chris selling garlic as well, but only Bob's price 30 (36 with the tax) is good enough for Alice whose budget is 50. The garlic of Chris with price 70 is too expensive for Alice.
Making logic programming privacy-preserving
An auction becomes more interesting if the underlying data can be sensitive. For example, a buyer may want to keep their proposed amount of money secret, so that the seller would not increase the price after seeing that the potential buyer is ready to spend more. It is also possible that a seller does not want to keep their product name public unless someone is directly interested in buying it. Finally, both buyers and sellers may want to keep their identities secret as far as there is no agreement on a certain bargain. A classic example of a privacy-preserving auction is the Danish sugar beet auction [4]. We want to achieve a more general task, and be able to answer Datalog queries while preserving the privacy of any involved data, including the inputs to the query.
A privacy-preserving application can be built on top of the Sharemind platform [5], which is developed by Cybernetica. With Sharemind, all input data is encrypted at the data source. Each individual value is split into random pieces that are distributed among several Sharemind Application Server computation nodes. None of the individual pieces provide any information about the original value. This process is called secret sharing and can be thought of as encryption without a key. No plaintext value leaves data owner's premises unencrypted.
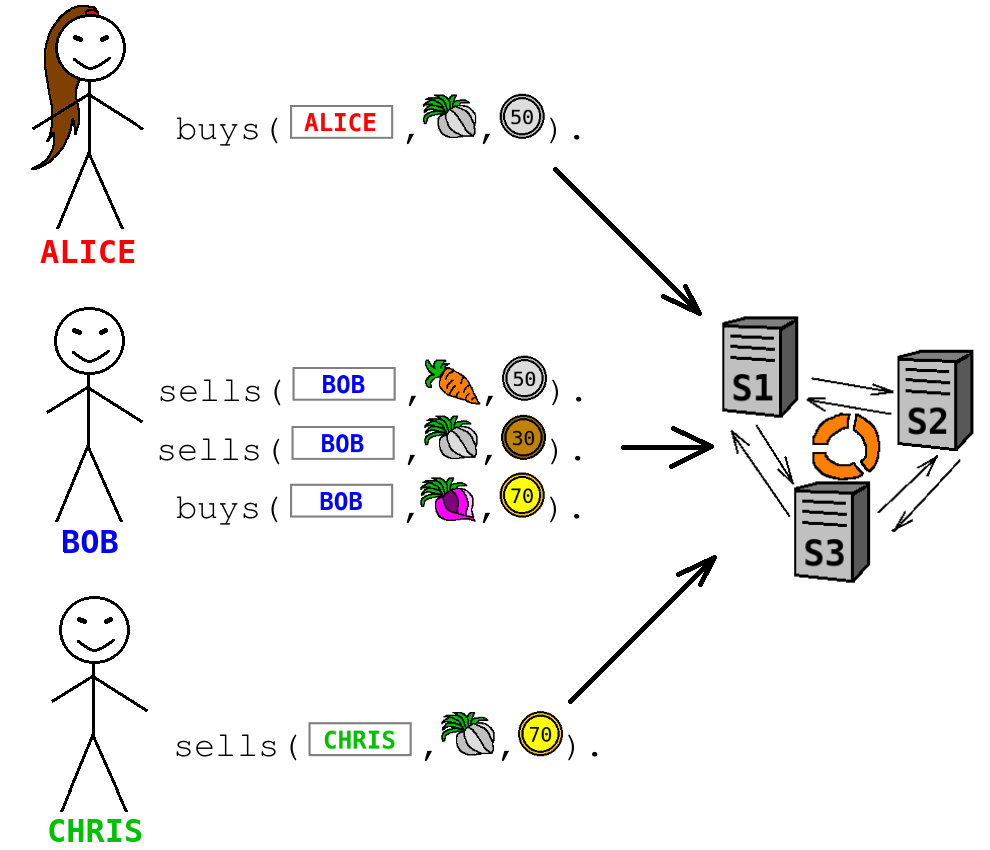
The basic programming language for writing Sharemind applications is SecreC, which is a C-like imperative programming language. While declarative languages like Datalog allow writing programs in a manner "what should be computed", in an imperative language developer has to describe "how the result should be computed". It is difficult to write efficient algorithms for Sharemind, since a developer needs to take into account the complexity of underlying cryptographic protocols that implement different operations. If one comes up with an optimal public algorithm (i.e. without preserving privacy), it is not necessarily optimal for Sharemind. For a beginner, it could be easier to write the program in a declarative language such as Datalog, delegating all optimizations to an automated tool.
As an outcome of the Estonian Research Council grant PSG497, we have come up with a translator from privacy-annotated logic programming scripts to Sharemind applications. Formally, we define a language PrivaLog (which stands for privacy-preserving logic programming), which is basically a variant of Datalog, equipped with data privacy annotations. Let us see how a PrivaLog script looks like on our running example. Instead of listing all instances of the facts ''buys'' and ''sells'' with public arguments, we describe only the structure of underlying data. Similarly, in the query statement, we do not write the name of the buyer and the product in plain but use placeholders.
:-type(sells(seller_name:private string, item:private string, price:private int)).
:-type(buys(buyer_name:private string, item:private string, price:private int)).
tax(Product, Tax) :-
Product = carrot,
Tax = 0.1.
tax(Product, Tax) :-
Product = garlic,
Tax = 0.2.
tax(Product, Tax) :-
Product = onion,
Tax = 0.3.
bargain(Buyer,Seller,Product) :-
buys(Buyer,Product,Budget),
sells(Seller,Product,Cost),
tax(Product,Tax),
Budget >= Cost * (1 + Tax).
?- bargain(input_buyer_name:private string, Seller, input_item:private string).
The database of buyers and sellers is uploaded into Sharemind in secret-shared manner in advance, using special data upload functionality of Sharemind. An automated tool transforms the PrivaLog script to SecreC code, which can then be executed on Sharemind platform.

Details of computation
Let us describe in more detail how the execution of a PrivaLog program works. In the beginning of computation, Alice provides secret-shared inputs ''input_buyer_name'' and ''input_item''. These values are treated as encrypted, and no Sharemind server learns that these are actually equal to ''alice'' and ''garlic'' respectively.

Sharemind uses provided inputs to find all solutions to the goal. In our example, Sharemind needs to find all possible values ''Seller'' satisfying the ''bargain'' rule.
?- bargain(input_buyer_name:private string, Seller, input_item:private string).
Sharemind should now follow the description of the rule ''bargain''. It needs to evaluate each condition of the rule, i.e. each line of the rule body. Let ''b1,...,b4'' be the bits that correspond to each of the four conditions, telling whether that condition is satisfied.
bargain(Buyer,Seller,Product) :-
buys(Buyer,Product,Budget), %b1
sells(Seller,Product,Cost), %b2
tax(Product,Tax), %b3
Budget >= Cost * (1 + Tax). %b4
Let us see how the satisfiability of each condition is computed.
- The first line extracts from the private database an instance of the fact 'buys'', and ''b1'' tells whether that instance matches the values ''Buyer' and ''Product''.
- The second line similarly extracts a fact ''sells'' and ''b2'' tells whether that fact matches the value ''Product''.
- The third line extracts a suitable ''Tax'' by matching ''Product'' against the product listed in one of the rules for ''tax'' (i.e. "carrot", "garlic", "onion"), and ''b3'' tells whether the matching has succeeded.
- The fourth line compares values ''Budget'' and ''Cost'', and ''b4'' tells whether the inequality holds.
All these comparisons depend on private data, so they are performed in a privacy-preserving manner (i.e. without revealing the compared values), and the results of comparisons ''b1,...,b4'' are secret-shared. The bit ''b1 & b2 & b3 & b4'' tells whether the particular combination of selected instances of ''buys'', ''sells'', and ''tax'' satisfies the rule, but since it is secret-shared, an unsatisfying solution cannot be discarded immediately. Eventually, Sharemind comes up with all possible secret-shared valuations of the variable ''Seller'' (which depend solely on the total number of instances of fact ''sells''), each valuation accompanied with a secret-shared bit ''b'' telling whether that valuation is satisfying.
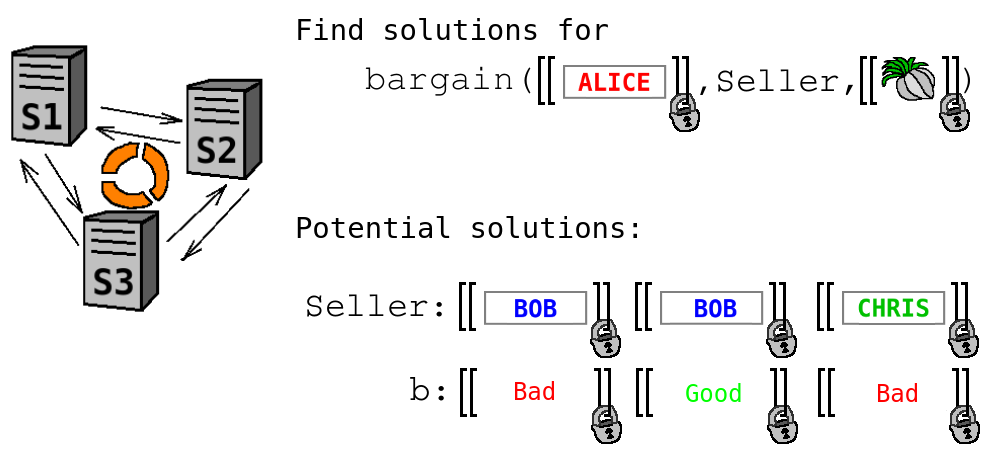
Sharemind system should now apply the filters ''b'' to the variables ''Seller'' and return the remaining valuations to Alice. However, the bits ''b'' are secret-shared and cannot be applied straightforwardly without revealing additional information. Hence, Sharemind should act as follows:
- Multiply ''Seller'' with ''b'' using private multiplication (i.e. without revealing neither ''Seller'' nor ''b''). Now each unsuitable ''Seller'' has been transformed to a constant ''0''. This ensures that Alice does not learn anything about unsatisfying solutions (e.g. that Chris was one potential seller).
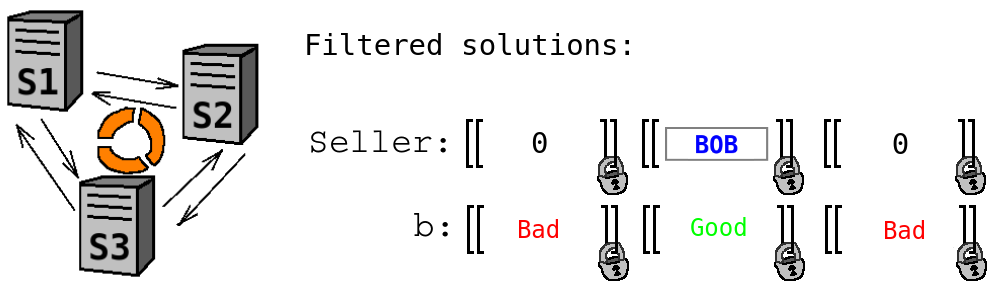
- Shuffle the solutions using private shuffle (i.e. without revealing the reordering permutation). This ensures that Alice will not learn the ordering of potential solutions. This can be important for privacy. For example, if Alice knows in advance that Bob was the first one who uploaded his data, and she learns that the satisfiable solution is the second one, then she can infer that Bob is selling some other product as well.
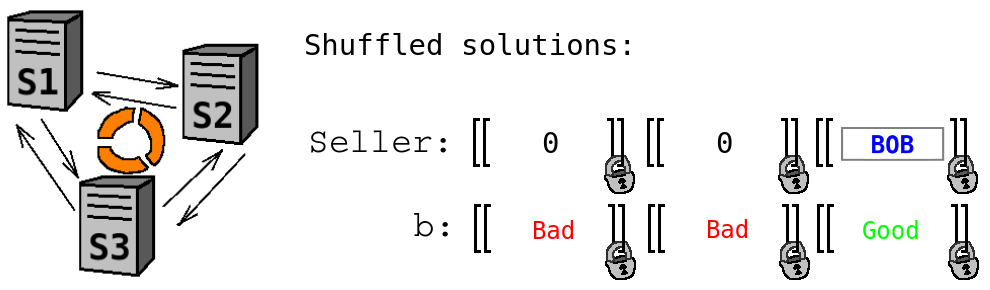
- It is now safe to send all pairs of ''Seller'' and ''b'' to Alice who will reconstruct these values from shares and do the filtering herself. However, in practice, there can be too many values that Alice actually does not need. For better efficiency, Sharemind servers can reconstruct the values ''b'', and send ''Seller'' to Alice only for satisfying solutions. Since all solutions have just been privately shuffled, such reconstruction reveals only the total number of satisfying solutions.
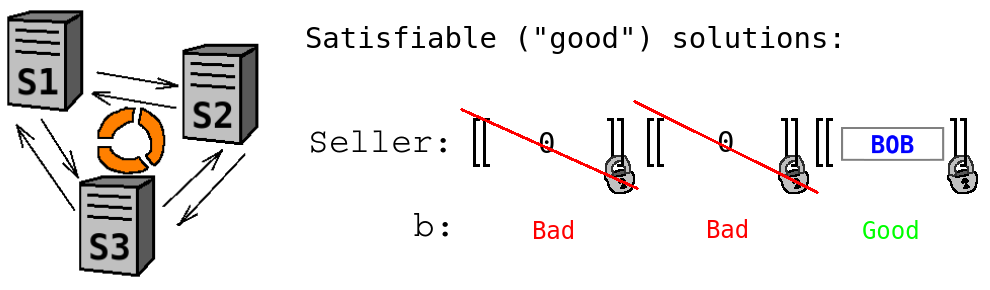
At the end of the computation, Alice receives a single valuation of the variable ''Seller'', which is reconstructed from shares on Alice's side, so that Sharemind servers will not learn that the final result was ''bob''.

More details about the translator can be found in related research papers [6, 7]. The implementation is available at github [8].
References.
[1] Krzysztof R. Apt. From logic programming to Prolog. Prentice Hall International series in computer science. Prentice Hall, 1997.
[2] Bramer, Max. Logic Programming with Prolog. Springer Science & Business Media, 2005.
[3] Stefano Ceri, Georg Gottlob, and Letizia Tanca. Logic Programming and Databases. Surveys in computer science.
Springer, 1990.
[4] Peter Bogetoft, Dan Lund Christensen, Ivan Damgård, Martin Geisler, Thomas P. Jakobsen, Mikkel Krøigaard, Janus Dam Nielsen, Jesper Buus Nielsen, Kurt Nielsen, Jakob Pagter, Michael I. Schwartzbach, Tomas Toft. Secure Multiparty Computation Goes Live. Financial Cryptography 2009.
[5] https://sharemind.cyber.ee
[6] Alisa Pankova and Joosep Jääger. Short paper: Secure multiparty logic programming. In 15th Workshop on Programming Languages and Analysis for Security (PLAS'20), 2020
[7] Joosep Jääger and Alisa Pankova. PrivaLog: a Privacy-aware Logic Programming Language. In 23rd International Symposium on Principles and Practice of Declarative Programming (PPDP'2021), 2021.
[8] https://github.com/fs191/secure-logic-programming
** This work was supported by the Estonian Research Council grant PSG497 **
