Precision is key when implementing and reasoning about security-sensitive systems. Whether it be the application of some cryptographic protocol, setting up a secure server, designing a database infrastructure, and more. Formal methods allow us to trust that such systems work as intended.
But it is rather limiting to think of such methods only applying to completely rigid and predictable systems. Much uncertainty stems from the real world, from random chance to the behaviour of humans, good or ill. A good formal system skirts this line between being precise and reliable yet adapting to the unpredictable behaviour of the environment.
By understanding constructive logic, the language of making guarantees, we can build rigorous systems which can describe the dependency on uncertainties and allow us to estimate the degree of trust we can put in the system.
Formal reasoning is all about being consistent. In a formal system, the rules of reasoning are established beforehand, and arguments are made using these existing rules. This makes the argument more trustworthy, as one is not allowed to change the rules when making an argument within the system.
Consequently, things proven within such a system are as robust as the system itself. So, if it has been established that the system is well-behaved, then this strengthens the arguments made using it.
Difference between classical and constructive arguments
The question of what makes a good formal system is not an easy one to answer. Since the beginning of the twentieth century, mathematicians have attempted to formulate the foundations of formal reasoning, resulting in various strands of logic. The most prominent of which is sometimes called classical logic.
With the advent of computers, more emphasis has been put on machine-readable proofs. These are arguments which can be interpreted and verified by a machine. This development has put more focus on constructive reasoning, which considers proofs as explicit constructions of evidence. Constructive logic originates from what is sometimes called intuitionistic logic, a name from before the time of computers, so-called since the creator Brouwer found the principles more intuitive than the principles of his fellow mathematicians.
One example of the difference between classical and constructive arguments lies in reasoning about "either or" statements. Take for instance the statement:
A classical reasoner may argue that this holds because there hasn’t been evidence to the contrary. A constructive reasoner however needs to provide stronger evidence and needs to proclaim which of the two options is true and give evidence for the chosen option.
They will construct a proof of “go to shop or home” by, for instance, first constructing a proof of “go to shop”, and then use the standard rules for “or” statements to conclude “go to shop or home”. However, this choice does not have to be fixed and can depend on other evidence.
The difference may seem small, but it has far-reaching consequences. Constructive arguments give more direct evidence for the truth of a property. This is useful when one wants to make stronger guarantees. Especially in the realm of security systems, it may be more dependable to build up guarantee and not merely prove we have found no way for it to fail.
Constructed proofs like this are also more adaptable, allowing them to be used in other contexts as long as the constraints of the guarantee are met. This in turn facilitates the construction of guarantees for bigger interconnected systems together.
The shape of an argument
Let's explore some of the rules of constructive arguments. The general statements we would like to express and prove have the following shape: we wonder whether a certain set of assumptions can be used to prove some consequence.
To do this, we need to lay down some ground rules by:
- establishing some basic truths
- formulating how arguments can be combined and fine-tuned.
As is usual in mathematics, we shall use letters “A, B, C, …” as variables. A letter is a placeholder for a statement, and we can replace a variable by a specific statement. They could really mean anything and are simply used to formulate general statements.
What we are most interested in is whether a certain collection of assumptions has a particular consequence. In this situation, both the assumptions and the consequence are expressed using a statement, and combined into what is called a sequent:
The word sequent is merely referring to the fact that the statement contains a sequence of assumptions. The above sequent states that from assumptions "A, B and C", we can conclude "D".
A classical reasoner would interpret this as an argument for: “Whenever A, B and C happen to hold, D inevitably holds”.
A constructive reasoner on the other hand will interpret this as: “From evidence for A, B and C, we can construct evidence for D”.
From the constructive perspective, you can think of a proof of a sequent as some algorithm which uses proofs of the assumptions as input and produces a proof of the conclusion. We see this as a function from assumptions to the conclusion. We may illustrate such a proof using a forked arrow as follows:
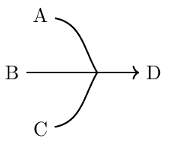
There are some basic reasoning principles which will hold, no matter the statements we reason about:
1.If the conclusion is assumed, the sequent holds. For instance, “A, B, C → B” is simply true. The proof as an algorithm simply returns the evidence of "B" it got as an input, “f(a,b,c) = b”.
2. A sequent will remain true if all you do is add more assumptions. So, if “A, B → D” is true, then so is “A, B, C → D”. Suppose we have an algorithm “f: A, B → D”. If we get evidence for "A, B and C" as input, we can take the evidence “a” and “b” of "A" and "B" and give that to "f", producing evidence “f(a,b)” of "D".
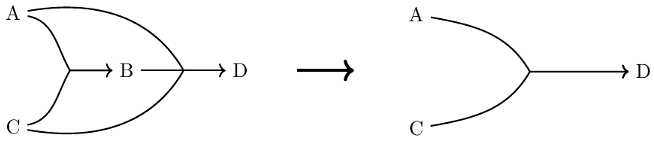
3. You can remove an assumption if you can prove it with the other assumptions. So, if “A, B, C → D” and “A, C → B”, you can conclude that “A, C → D”. As an algorithm, given “f: A, B, C → D” and “g: A , C → B”, then we can turn evidence “a” and “c” of "A" and "C" into evidence of "D" by taking “f(a, g(a,c), c)”. Here is an illustration of this principle:
Composite statements
Let us consider more concrete statements, going beyond mere variables. Generally, logical statements can be given an interpretation by answering the questions:
- How can we prove the statement?
- How can we use the statements to prove other things?
The answers to these questions can then be translated into sequent expressing:
- What assumptions are sufficient for concluding a statement?
- In what way can the statement be used as an assumption to prove other results?
We start with a simple example. We write “A /\ B” to say that both statements “A” and “B” hold. Let us ask ourselves the two questions from above and turn them into sequents.
How do we prove “A /\ B”?
To provide evidence of the fact that both “A” and “B” holds, we need to provide evidence for both. As such, if we can prove “A” and we can prove “B”, we should be able to prove “A /\ B”.
This can be changed into the sequent “A, B → A /\ B”.
How can we use “A /\ B” to prove other statements?
If we have evidence of “A /\ B”, we must have evidence of both “A” and “B”. So, we can simply say that the sequents “A /\ B → A” and “A /\ B → B” are true.
This allows us to then use “A” and “B” in further proofs.

Let us also return to our “shop or home” example from before, by considering “or” statements. We write “A \ / B” to say either “A” holds or “B” holds.
How to prove “A \ / B”?
To provide evidence of the fact that either “A” or “B” holds, we need to provide evidence of either “A” or “B”. So, if we can prove “A” then we can prove “A \ / B”, and if we can prove “B”, we can also prove “A \ / B”.
This can be turned into sequents “A → A \ / B” and “B → A \ / B”.
How can we use “A \ / B” to prove other statements?
If we have evidence of “A \ / B”, then we have evidence either for “A” or for “B”, but we need to be ready for each case. The situation may be uncertain and needs to have a response for both possibilities.
The general proof principle is: if we can prove something using “A”, and we can prove the same thing using “B”, then we can prove it using “A / B”. In terms of sequents, we can say that if “A, C → E” and “B, C → E”, then “A \ / B, C → E”.

For instance, we can prove the sequent “A /\ B → B / C” by first reasoning that we can prove the or statement with “B → B \ / C” which can be extended using principle 2 by assuming more: “A /\ B, B → B \ / C”. We then argue that we can combine this statement with “A /\ B → B” using principle 3, to prove one assumption with the other. This results in the sequent “A /\ B → B \ / C”.
The use of computers
Though the above argument is logically sound, it is not entirely satisfactory. You may have found yourself trying to follow along with the argument and verifying that it is correct. But we would prefer that the argument itself is more self-evident. The problem is that we already need a kind of reasoning system to check the argument.
This gets us into a philosophical chicken and egg problem of what comes first, trying to establish a system of reasoning using another kind of reasoning. What is the difference between “A \ / B” and saying “A” or “B”? What is the difference between saying from “A” we derive “B” and the statement “A → B”.
These questions get in the way of developing a formal theory. This is why we should establish a solid foundation for our reasoning system, to avoid ambiguity regarding this very fact.
One solution is to use computer-verifiable proofs and let the computer check the validity of an argument. The loose and wordy reasoning style used above can instead be transformed into the simple question: Can we construct an algorithm turning evidence of the assumptions into evidence of the conclusion?
Instead of reasoning rules, we formulate program construction rules, changing the act of proving guarantees into a program design problem within some domain specific language. The question of whether the program is well-constructed can then be verified using type-checking.
Those familiar with algebraic data types may recognise some of the arguments we used as introduction and elimination rules for particular data types. We can see “A /\ B” as a pairing type, pairing something of type “A” with something of type “B”. On the other hand, “A \ / B” can be seen as a sum type, which contains both stuff from types “A” and “B”. This correspondence between types and statements, programs and proofs is what is known as the Curry-Howard correspondence.
Adding context to assumptions
Before we end this post, let me illuminate the flexibility of reasoning with logic and domain specific languages.
We started this post explaining how logic can facilitate trust in an application, despite uncertainties. In today's interconnected world, we operate on a lot of assumptions, and not all can be personally verified. As such, it is useful to put certain statements in context:
- Who has made the statement?
- Where was the statement shared?
- When was the statement shared?
This helps evaluate such statements, and treat them not as simply true, but as true within the context in which it was made.
We can add context using modalities, which like “and” and “or”, are operations in our space of statements. For instance, we can use the modality “Cyb” for statements which were officially made by Cybernetica. Then “Cyb(A)” is the statement that Cybernetica claims “A” is true.
People can now use this statement within their own system, without having to assume that “A” itself holds. You can construct guarantees using other people’s statements, allowing you to evaluate them and determine whether these are trustworthy.
The main assumption we make for reasoning about contexts is that we can always combine statements made in the same context, and that we can logically reason within every context. This is all wrapped into the single rule on sequents which is:
This way we can derive consequences of the combined collection of statements made by an entity, which in turn helps us build stronger guarantees.
Basically, if we know Cybernetica has made statements “A”, “B”, and “C”, then they are implying the truth of “D”. We can prove this by gathering the statements made in that context and then simulating reasoning within that context.
As a program, think of the assumptions as locked resources which can be unlocked once we start constructing a statement within the context of “Cyb”.
Further assumptions can be made regarding which context is aware of which other context, factors that depends on their place and time. This kind of awareness is passive and happens regardless of the information being actively shared.
For instance, one may assume that for any statement “A”:
“Internet(A) → Cyb(Internet(A))”
This could be assumed to hold, since Cybernetica has access to the internet and can refer to sources on the internet when making statements. Note that this does not mean Cybernetica is making the claim “A” or saying it is true. They are merely referring to it within its proper context.
On the other hand, you can specify whether you trust a certain context regarding a particular statement. For instance, for a particular statement “A” we can state: “Cyb(A) → A”
This formally states that if Cybernetica claims “A” is true, then it must be true, and hence relays trust in “Cyb”. This trust is dependent on the particular content of the statement “A”. So, you may believe Cybernetica whenever they post something regarding post-quantum yet not readily accept whatever they are on about in this blog post on constructive logic.
That’s all for now
In conclusion, by creating a formal system of reasoning we can construct guarantees we can rely on, to ensure the safety and robustness of a system. With composite statements, we can formulate more complex situations, combining multiple properties into one. Moreover, with modalities, we can put statements into context, declaring who claims or believes that a statement is true.
One of the ways we use this kind of reasoning at Cybernetica is in the analysis of trust. In distributed and collaborative systems, you need to analyse and combine claims from different sources. Which sources do you need to trust to prove the guarantee?
Having dealt with all the tedious logic stuff, what is left is a simple statement: We can make a guarantee if we are willing trust these sources. With this objective mathematical truth out of the way, we can move towards the more subjective sociological question of whether we should trust the sources.
In ongoing work, we analyse how we can derive which sources we need to trust in order to make a certain derivation. Deriving such collections of sources is discussed in a forthcoming paper “Threshold Trust Logic”. Moreover, since we work with a constructive logic, we can employ computer assistance to find proofs of statements, with algorithms guaranteed to derive a proof if a proof exists in “Forward Proof Search for Intuitionistic Multimodal K Logics”.
We are working on applying this kind of reasoning to a variety of distributed systems, including trust pipelines for software, public key infrastructures, and electronic voting systems.
