Cybernetica was granted funding by DARPA (Defense Advanced Research Projects Agency) under PROVENANCE (PROofs and Verifications between governmENts ANd CitizEns) project to bring value to communication between the public and private sector by creating techniques for constructing meaningful zero-knowledge proofs. The goal is to improve government interactions with citizens, companies, and other governments by enabling them to confidentially handle sensitive data.
Zero-knowledge proofs
We use a variety of cryptographic techniques for our information security needs. For most of these techniques, we intuitively understand what security properties they achieve and why it is reasonable to expect that such properties can be achieved. Encryption of a message corresponds to putting it into an opaque envelope. Signing a message corresponds to attaching something that could have only been created by the signer to the message. The cryptographic techniques for these actions use mathematical transformations where no-one knows reasonable inverse transformations (unless some trapdoor is present). Another technique — identification — is similar to passing a face-check or telling a guard the password.
Zero-knowledge (ZK) proofs are one of these cryptographic techniques with apparently magical properties, mixing privacy and integrity in a manner that seems impossible. These proofs allow one party — the prover — to convince another party — the verifier — that a statement holds. If the statement actually does not hold, then a cheating prover is not going to be able to convince the verifier. On the other hand, the verifier learns nothing about why the statement holds, it will only learn that it does hold. It is hard to imagine something in the physical world having similar properties.
A lot of work in improving the efficiency of ZK proof techniques has been done since they were first proposed in 1985 by Shafi Goldwasser, Silvio Micali, and Charles Rackoff. We are on the verge for having practical proofs for statements that we actually want to prove in ZK. Indeed, we are already using ZK proofs in a number of applications. Zero-knowledge protocols for identification, convincing the verifying server that the client knows the correct password but giving it no information about what the password actually is, were already proposed in early 1990s. In these protocols, the initial knowledge of parties, and the likely flow of messages and information is depicted below.
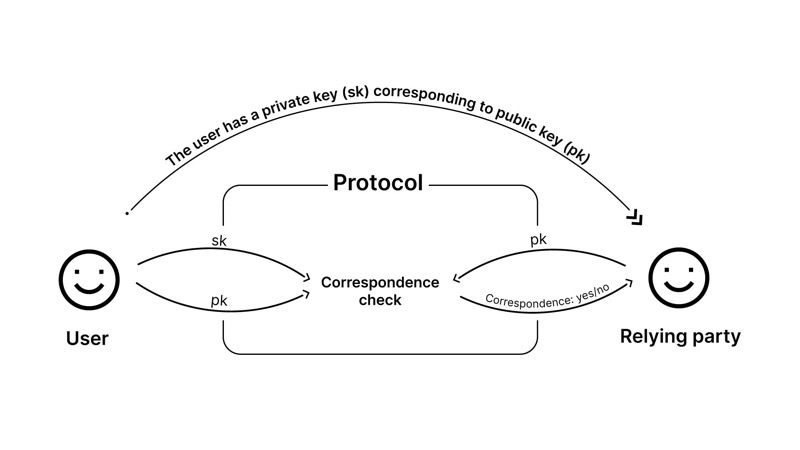
In such identification protocols, the user has typically generated (either himself, or proxied it to some enrollment service) a public and private key pair (pk , sk ), announced the public key pk to everyone (typically through the use of certification services), and kept the private key sk to himself. The public key pk could be a random element of some cyclic group G of size p with hard discrete logarithm (e.g. some elliptic curve group, like the one we use on our identity cards), generated by one of its elements P. Here the group G being cyclic and the element P generating it means, that the values P, P +P, P +P +P, etc., enumerate the entire group G The private key corresponding to pk is sk ∈ {0, . . . , p − 1}, that is the discrete logarithm of pk, meaning that sk · P = pk. Here the notation sk · P means that we add up P + P + · · · + P for a total of sk times. In a simple identification protocol, User generates another random value r ∈ {0,...,p − 1}, computes α = r · P and sends it to Relying Party. The Relying Party responds with yet another random value b ∈ {0, . . . , p − 1}, and finally User sends the number m= (r+b·sk) mod p. Relying Party accepts if m·P =α+b·P.
It is easy to see that Relying Party does not learn anything new during the protocol. Indeed, whatever he learns, is surely contained in the messages that he sees while executing the protocol. He sees a triple of (random) values (α, b, m), having a certain distribution, and a certain relationship among each other and with the value pk. In order to generate such triples with such distribution, the involvement of User is not necessary at all. Indeed, one can first generate the value b; it is uniformly randomly distributed over the set {0, . . . , p − 1}. As next, one can generate the value m, which is independent of b, and also uniformly randomly distributed over the set {0, . . . , p − 1}, because in the actual protocol, it has the additive dependency of r that is distributed like this. Finally, after generating b and m, there is a single possible value for α that makes Relying Party accept, and it can be computing from the acceptance check as α= m·P − b·pk.
It is a bit more complex to see that User has to know the value sk in order to convince Relying Party. This follows from the fact that after User has sent the first message α, he must be ready to answer several different possible challenges b. If User is then able to answer a challenge b with m, and a different challenge b′ with m′ (i.e. m · P = α + b · pk, and m′ · P = α + b′ · pk), then the values b,b′,m,m′ determine sk . Indeed, we have m · P − b · pk = m′ · P − b′ · pk (because both sides of this equality are equal to α); if we consider this equality as an equation between multipliers of P (as pk = sk · P ) and rearrange, then we obtain sk = (m − m′)/(b − b′), where the division means the multiplication with the reciprocal of the divisor modulo p.
Currently, we are also using ZK proofs in internet voting, specifically in mix-nets used during the tallying of votes, corresponding to shaking of the ballot box in order to mix up the ballots. Even more complex statements (if not by size, then at least by structure) can be found in crypto-asset management, where privacy-preserving updates to distributed ledgers are accompanied by proofs of consistency.
We can think of significantly more complex statements that we may want to prove in zero-knowledge. A prime example is the knowledge of a zero-day exploit for some piece of software. Here the prover is a security researcher who has determined an input that brings this piece of software to an undesired state. The verifier is the maintainer of that software. Their common input is the code of that piece of software (either source code or the object code, whatever the security researcher has worked on), and also the description of undesired states (e.g. stack overflow, or segmentation fault). The statement being proven claims, that there exists an input to the given piece of software, such that after a given number of execution steps, a state is reached that matches the description of undesired states.
With the statements to be proved getting more complex, this is where Cybernetica’s PROVENANCE project comes in. In this project, we provide tools to precisely specify the statement being proved, the parameters of a particular proof instance, and the actual verification procedure of a purported proof. These tools are centered around a programming language for statements and proofs, which are compiled into an intermediate representation where they can be ingested by a variety of cryptographic techniques for ZK proofs. The tools we develop in PROVENANCE will benefit from our decade-long experience of constructing similar specification tools for secure multiparty computation.
The ZK-SecreC programming language, developed in PROVENANCE, provides means to express the business logic and the statements to be proven in a way that both provides a high level of abstraction whenever possible and makes explicit the details that have to flow down to the ZK proof techniques in order to make them efficient. Our tools allow to specify which parts of the statement are known to both the prover and the verifier (and possibly to third parties that a concrete cryptographic technique uses in order to make the proofs more efficient) and thus do not have to be hidden, and which parts are part of the secret witness. ZK-SecreC is an expressive high-level language, inspired by our SecreC language for secure multiparty computation, for stating how the pieces of business logic are combined in a statement that is to be proven in ZK. The statements in that language can be linked with programs and executable specifications in other languages, as well as argue about the static and dynamic properties of these specifications. We can see that there are operations that the ZK proof techniques can handle in a particularly efficient manner, eventually ZK-SecreC will contain primitives to directly access these operations. In particular, we have in mind the verifications of attestations (signatures, time-stamps, commitments, ZK proofs, etc.). Altogether, PROVENANCE translation tools will bring the complexity of constructing complex statements close to writing a series of SQL queries, but without compromising on the efficiency of the created circuits and resulting ZK proofs.
In PROVENANCE, we demonstrate the usefulness of ZK-SecreC and associated tools through demonstrators for relatively complex scenarios. In our first scenario, a recruit is compiling the medical evidence which may or may not disqualify him from service, and will prove to the recruitment office in zero-knowledge that he is holding the evidence signed by healthcare providers. The challenges here have been verification of digital signatures and parsing of digital documents, all done as part of process- ing of the prover’s input to the ZK proof. In our second scenario, we intend to show in zero-knowledge that a sensitive network log does or does not contain an evidence of a cyberattack. Here our challenge is to handle the possibly great length of the log, making the size of the statement less dependent on it. Our third scenario is about presenting an alibi against a person being in a certain place at a certain time, doing it in zero-knowledge, such that the exact reason underlying this alibi will not become public. Here the main challenge is the great heterogeneity of possible grounds for the alibi, all of which have to be handled by our tools.
Distribution Statement "A" (Approved for Public Release, Distribution Unlimited).
PROVENANCE has been funded by the Defense Advanced Research Projects Agency (DARPA) under contract HR0011-20-C-0083. The views, opinions, and/or findings expressed should not be interpreted as representing the official views or policies of the Department of Defense or the U.S. Government.
More information about the project: https://cyber.ee/research/projects/provenance

