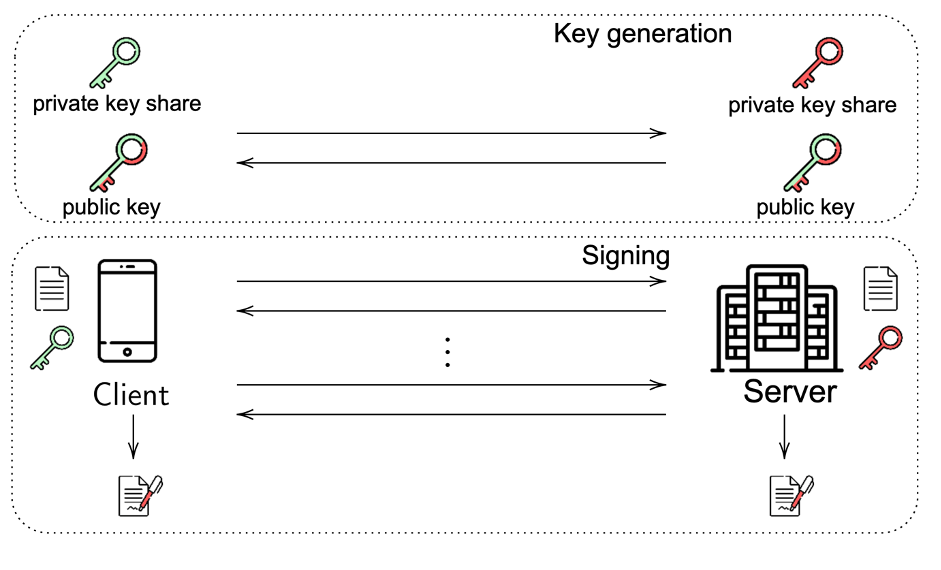
SplitKey is a solution for authentication and creation of digital signatures with the user’s mobile device. It relies on threshold cryptography to provide secure storage of the private key that is needed to create digital signatures. The main idea behind the usage of threshold signatures in SplitKey is the following:
- User’s mobile device (client) and supporting server engage in interactive key generation protocol. Mobile device generates one share of the private key and the supporting server generates second share of the private key. Through the message exchange, they establish a single combined public key.
- When the user needs to create a signature, the mobile device applies their share of the private key to the message to create a signature share and sends it to the server. The server then applies their share of the private key to create the final signature.
- The signature generated using this interactive protocol will be verified using a single combined public key that was generated by the mobile device and server. Moreover, the signature looks like a standard signature, i.e., the verifier does not need to know that it has been created using the SplitKey protocol. To the verifier, the public key and the signature look as if they have been produced by a non-threshold version of the signature scheme.
The security intuition behind this solution is that neither the user’s device nor the server can create valid digital signature without interacting with each other. Even if the attacker gets access to the private key share from the user’s device, they will not be able to create signatures without the supporting server. Similarly, the server alone (or perhaps an attacker that has taken over the server) cannot create a valid signature. Moreover, supporting server has an additional mechanism to detect malicious behaviour if the user’s key share has been cloned.
Currently used solution relies on the RSA signature scheme, which is not quantum-safe. Therefore, there is a need to switch underlying signature scheme to the post-quantum alternative. The signature scheme should be selected from the schemes that will be in accordance with NIST standards to provide the standard compliance. Thus, currently, there are three schemes to select from — Crystals-Dilithium, Falcon, and Sphincs+.
Although Sphincs+ provides conservative security guarantees, it is a less efficient scheme with large signatures (7856 byte signature for approximately the same pre-quantum security as RSA3072). Additionally, its design does not support easy distribution of the key generation and signing algorithms. Falcon provides smaller signatures (666 byte signature for approximately the same pre-quantum security as RSA3072), but has quite complicated design, requiring operations with floating-point arithmetics for efficiency and is more prone to the side-channel attacks. Since the structure of Crystals-Dilithium signature seems to be the most friendly for distributing between two parties, we decided to work with it.
Even though Crystals-Dilithium structure supports some of the multi-party computation techniques, it also has its caveats. The most challenging part being related to the so-called rejection sampling. When the Crystals-Dilithium signature is generated, it needs to pass several checks that verify that the signature does not leak information about the private key. If any of those checks are not passed, the signing process starts from the beginning until the valid signature is produced. The parameters of Crystals-Dilithium have been selected so that the average number of restarts needed to produce a valid signature is 3-4. This does not complicate the regular signature too much, because all the computations are done locally and it is not costly to restart the signing process a couple of times. However, if one would distribute the signing process, more questions arise:
- Is it secure to show some intermediate computations to the other party before we learn whether signature would be rejected?
- How many times would we need to restart protocol until all the conditions are met on both sides?
- How to deal with compression techniques?
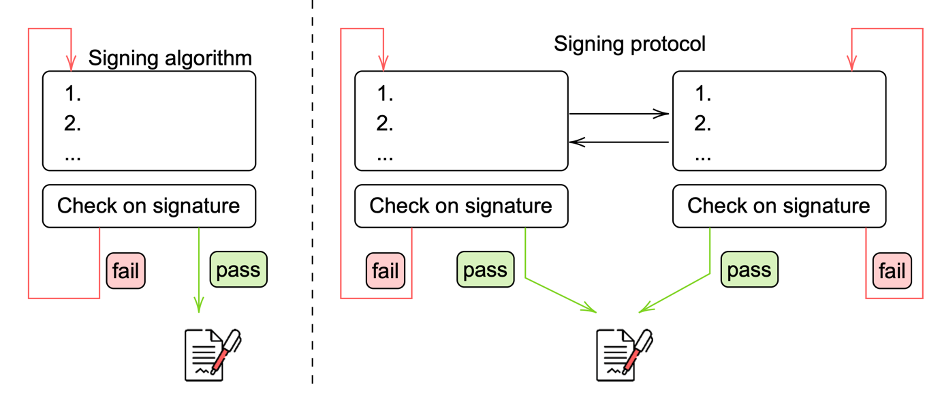
Our solution tries to tackle all the above-mentioned questions, but at a cost that the final signature is not exactly a Crystals-Dilithium signature. To deal with the first problem, we perform intermediate computations under the commitments. What does it mean? The user’s device and server do not send intermediate values computed during the signing process as plaintext, but commit to them, hiding the content from the other party. Due to the special property of the commitment scheme that we use, we can perform simple computations (addition) directly on the commitments. And once the rejection sampling is performed on the signature and parties learn that the signature does not leak the private key, the commitments can be opened and verified.
To deal with the second problem, we propose to generate multiple instances of the protocol simultaneously and then combine values from the different instantiations until the combination that passes the rejection sampling is found. This would eliminate the need to restart the signing protocol with all the intermediate communication rounds many times. However, this approach results in the increased amount of data that needs to be exchanged between the client and the server.
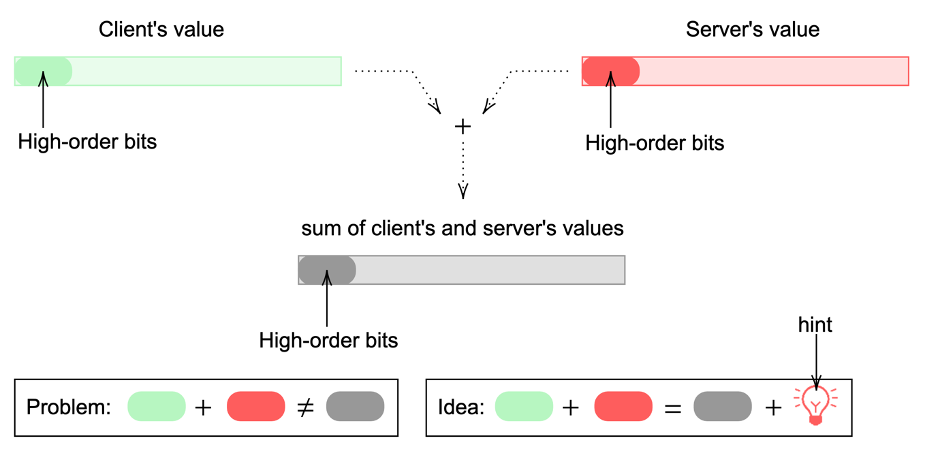
The third problem is a bit more exquisite. Crystals-Dilithium signature scheme makes use of bit decomposition techniques to compress the size of the public key and signature. The idea is that for some computations knowing just the high-order bits of some value would be enough. Thus, this saves some storage as one would need to keep only the high-order bits instead of the whole value itself. However, those bit decomposition algorithms do not have the same beautiful property as the commitments that we discussed above. We cannot just add the high-order bits of two values hoping that this will be equal to the high-order bits of the sum. Our trick is to use a special hinting technique, a bit similar to the one from the Crystals-Dilithium. The hint that the parties can compute out of the public values, tells whether the bit flip in the high-order bits has happened which allows to adjust the values during the verification.
Due to the techniques we needed to use for the first and the third questions, the signature that is produced with our protocol is not the same as the Crystals-Dilithium signature — it contains commitment value and our special hint. Therefore, the verification algorithm specified in the Crystals-Dilithium will be unable to verify our signatures. The next big question that we are trying to tackle — is it possible to produce Crystals-Dilithium signature using some different cryptographic techniques?
